To view the temperature profile for this situation, click on the following link: Matlab Heat Exchanger Program

Part B:

> U1:= 50*(Btu/(hr*ft^2*F)); U2:= 350*(Btu/(hr*ft^2*F)); Th1:= 150*F; Th2:= 250*F; Tc1:= 80*F; Tc2:= 182.857*F;

> A:= 'A';

> A:= (-Qhspec)*(((U1*(Th2-Tc2) - U2*(Th1-Tc1)))/(ln((U1*(Th2-Tc2)/(U2*(Th1-Tc1))))))^(-1);

Part C:

The key to this problem is that the oil and water temperatures a surface 2 will be the same.

For counterflow:

> Tc2:=250*F;

> wc:='wc';

> Qc:=wc*Cpc*(Tc2-Tc1)=-Qhspec;

> wc:=solve(Qc,wc);

For parallel flow:

> wh:=12000*(lbm/hr);wc:='wc';Cph:=0.6*(Btu/(lbm*F));Cpc:=1.0*(Btu/(lbm*F)); U0:=200*(Btu/(hr*ft^2*F));

> Th1:=250*F;Th2:=150*F;Tc1:=80*F;Tc2:= Th2;

> Qh:=wh*Cph*(Th2-Th1);

> Qc:=wc*Cpc*(Tc2-Tc1)=-Qh;

> wc:=solve(Qc,wc);

Part D:

Executing example 15.4-2 for parallel flow:

> restart;

> eqh:=w*Cph*D(Th)(z)=U0*2*Pi*r0*(Tc(z)-Th(z)); Balance on the hot side using eq. 15.4-10 and eq. 13.1-8.

> eqc:=w*Cpc*D(Tc)(z)=U0*2*Pi*r0*(Th(z)-Tc(z)); Balance on the cold side.

> s:=dsolve({eqh,eqc,Tc(0)=Tc1,Th(0)=Th1},{Tc(z),Th(z)}):

> assign(s); Th:=unapply(Th(z),z);Tc:=unapply(Tc(z),z);

Temperature changes for parallel flow:

> dT1:=simplify(Th(0)-Tc(0));

> dT2:=simplify(Th(L)-Tc(L));

> log(dT1/dT2);

> logdT12:=simplify(%,assume=positive); Agrees with eq. 15.4-14

> Cpc:=-Qh/(wc*(Tc2-Tc1)); Using eq. 15.4-9 and the fact that Qc=-Qh.

> Cph:=Qh/(wh*(Th2-Th1)); Using eq. 15.4-8.

> logdT12;

> Qc:=solve(-logdT12=logdT21,Qh); eq. 15.4-15

In this last expression, logdT21 is log(dT2/dT1) which is -log(dT1/dT2) or log((Th2-Tc2)/(Th1-Tc1)). Therefore, for parallel flow, Qc is:

> Qc:=(UA,Tc2,Tc1,Th2,Th1)->UA*((Th2-Tc2)-(Th1-Tc1))/log((Th2-Tc2)/(Th1-Tc1));

> wh:= 12000*(lbm/hr); wc:= 12000*(lbm/hr); Tc1:=80*F; Th1:=250*F; Th2:=150*F ; Cpc:=1*(Btu/(lbm*F)); Cph:= 0.6*(Btu/(lbm*F)); Uo:= 200*(Btu/(hr*ft^2*F)); These are the parameters given in the problem.

> Qhspec:=wh*(Th2 - Th1)*Cph;

> Tc2:=(solve(-Qhspec=wc*(Tc2-Tc1)*Cpc,Tc2));

> UA:=solve(-Qhspec=Qc(UA,Tc2,Tc1,Th2,Th1),UA);

> A:= UA/Uo;

Plotting temperature profile:

> simplify(Th(zeta*(A*Btu*w/r0/F/U0/Pi/ft^2/lbm))/F);

> simplify(Tc(zeta*(A*Btu*w/r0/F/U0/Pi/ft^2/lbm))/F);

> plot({Th(zeta*(A*Btu*w/r0/F/U0/Pi/ft^2/lbm))/F,Tc(zeta*(A*Btu*w/r0/F/U0/Pi/ft^2/lbm))/F},zeta=0...0.01,color=[red,blue]);

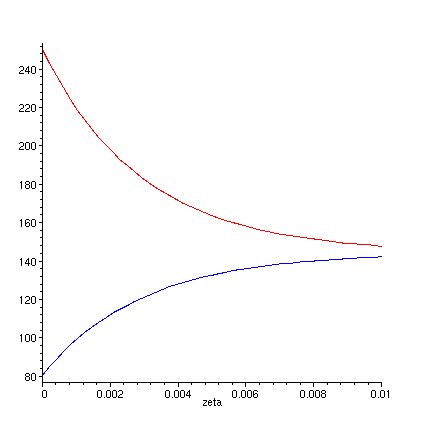
As one can see, this is a very inefficient way to operate a heat exchanger because the temperature differnce tends to converge and is not constant throughout the heat exchanger..