Example 15.4-3: Power Requirement for Pumping a Compressible Fluid Through a Long Pipe

from Bird, Stewart, & Lightfoot, Transport Phenomena, 1960, p. 467.

Nathaniel Chongsiriwatana and Steve Meier

CENG 402: Transport Phenomena II

Spring 2001

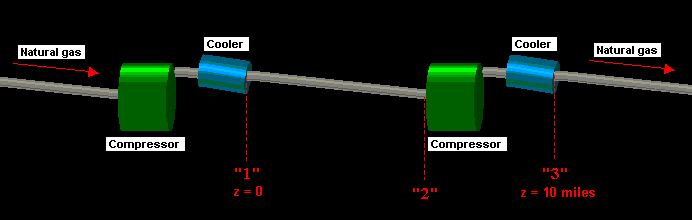
Figure 1.  Pumping natural gas through a pipeline. Pumping stations spaced at intervals of 10 miles recompress and cool the fluid to its original temperature and pressure.

A natural gas, which may be considered pure methane, is to be pumped through a long smooth pipeline with a 2-ft inside diameter.  The gas enters the line at 100 psia at a velocity of 40 ft/sec and at the ambient temperature of 70° F.  Pumping stations are provided every 10 miles along the line, and at each of these stations the gas is recompressed and cooled to its original temperature and pressure (see Figure 1). Estimate the power that must be expended on the gas by each pumping station, assuming ideal gas behavior, flat velocity profiles, and negligible changes in elevation.

In solving this problem, one should consider the pipe and compressor separately.  The first step is to apply Bernoulli’s Equation in differential form to a length element dz of the pipe.  This equation is then integrated between planes “1” and “2” to obtain the unknown pressure p2.  Once p2 is known, we again apply Bernoulli’s Equation to the system between planes “2” and “3” to determine the work done by the pump.

Bernoulli’s Equation (15.2-3):

            [1]

Because we are assuming flat velocity profiles, we can replace the quantity <v³>/<v> to a very good approximation with <v²>. Also, there are no potential energy considerations and there is no work done on the pipeline, and by definition:

                                           [2]

If we then write the equation in differential form, we obtain:

> bernoullieq1:=v*dv+1/rho*dp+1/2*v^2*f/R[h]*dz=0;

R_h is given by the cross section of the pipeline divided by the wetted perimeter (equation 6.2-16).

> R[h]:=(pi*d^2/4)/(pi*d);

> bernoullieq1:=expand(bernoullieq1/v^2);

We assume the methane can be described by the ideal gas equation of state. In addition, a mass balance allows us to solve for r and v in terms of other variables.

> eqnofstate:=p=rho*R*T1/M[w]; massbal:=rho*v=rho1*v1;

> s:=solve({eqnofstate,massbal},{rho,v}); assign(s);

Define both the differential change in velocity and r₁ to further simplify the Bernoulli equation.

> dv:=diff(v,p)*dp; rho1:=p1*M[w]/(R*T1);

Because the pipe is long, we can assume the flow to be isothermal, thus

> T:=T1;

Section 1.3 showed that the viscosity of ideal gases is independent of pressure. As a consequence, the Reynold's number, defined as:

is also constant, since the system is isothermal. Because Re is constant, the friction factor f is also constant. The Bernoulli equation thus simplifies down to a form independent of density, and identical to equation 15.4-18:

> bernoullieq1;

Integration of the first two terms from p=p₁ to p=p₂ and the last term from z=0 to z=L gives

> bernoullieq1:=-ln(p2/p1)+1/2*R*T1/M[w]/v1^2*((p2/p1)^2-1)+2*f*L/d;

In order to find f , we need to calculate the Reynolds number

> RE:='v1'*d/nu; where n is the kinematic viscosity =m / r

> v1:=1219.2; [cm/sec] (a.k.a. 40 ft/sec)

> d:=60.96; [cm] (a.k.a. 2 ft)

> nu:=2.424769e-2; [cm²/sec] n for methane at 100 psia and 70 F (a.k.a. 2.61e-5 ft²/sec)

> RE;

We can use this Re in conjunction with the graph of f vs Re on p. 186 of B, S, & L (Fig. 6.2-2) to find

> f:=.0025;

Additionally, we are given that

> M[w]:=16.0426; [g/mol] for methane

> T1:=294.261; [K] (a.k.a. 70 F)

> L:=1609344; [cm] (a.k.a. 10 miles)

> p1:=100; [psia]

> R:=8.3144e7; [g*cm^2*/sec^2/mol/K]

> s:=solve(bernoullieq1,p2);

> p2:=s[2];

Part (b) - Flow through the compressor

> restart;

Now we can use Bernoulli's equation in the form to obtain the work done by the compressor:

                     [3]

> bernoullieq2:=(1/2)*(v3^2-v2^2)+Int(1/rho,p=p2..p3)+Ev=-W;

If we assume the compression is adiabatic, pr^-g is a constant. We call g " g1" in this worksheet because plain g is a "protected" variable in MAPLE.

> eq1:=p*rho^(-gamma1)=p2*rho2^(-gamma1);

> rho:=solve(eq1,rho);

If we assume that we can neglect Ê_v through the compressor, the Bernoulli equation becomes:

> bernoullieq2:=(1/2)*(v3^2-v2^2)+int(1/rho,p=p2..p3)=-W;

Substitute in for p₂ using the ideal gas law.

> p2:=rho2*R*T2/M[w];

> bernoullieq2;

Since the compressor cools the gas to its original temperature and pressure, p₁ must equal p₃. The same is true for the velocities v₁ and v₃.

> p3:=p1; v3:=v1;

The equation simplifies to...

> bernoullieq2;

The mass flow rate at point 1 is equal to the mass flow rate at point 2, thus:

> v2:=rho1*v1/rho2;

> bernoullieq2;

Substitute in for r₁ and r₂ using the ideal gas law.

> p2:='p2':

> bernoullieq2:=subs(rho1=p1*M[w]/(R*T1),rho2=p2*M[w]/(R*T2),bernoullieq2);

The flow is isothermal, thus T₁ = T₂.

> T1:=T2;

The final equation is:

> bernoullieq2;

Compare with the book's equation 15.4-23.

> bookeq:=v1^2/2*(1-(p1/p2)^2) + R*T2/M[w]*gamma1/(gamma1-1)*((p1/p2)^((gamma1-1)/gamma1)-1);

They are equal.

> simplify(expand(bookeq-lhs(bernoullieq2)),assume=positive);

Input given values:

> d:=60.96; [cm] (a.k.a. 2 ft)

> v1:=1219.2*cm/sec; [cm/sec] (a.k.a. 40 ft/sec)

> M[w]:=16.0426*g/mol; [g/mol] for methane

> T2:=294.261*K; [K] (a.k.a. 70° F)

> p1:=100; [psia]

> p2:=86.16233216; [psia] (from Part (a))

> R:=8.3144e7*g*cm^2/sec^2/mol/K; [g*cm²*/sec²/mol/K]

Calculate g. The heat capacity was found using data from the NIST webbook.

> Cp:=35.6; Cv:=Cp-8.314; gamma1:=Cp/Cv;

> W:=solve(bernoullieq2,W);

Using the FORTRAN program convu, we find that this equals

> W:=-7724.113*ft*lb[f]/lb[m];

Redefine R in different units

> R:=1.5443e3*ft*lb[f]/mol/Rank;

Redefine variables in units of Rankine, feet, and pounds.

> T2:=529.67*Rank;

> d:=2*ft;

> v1:=40*ft/sec;

> p1:=100*lb[f]/inch^2*(12^2*inch^2/ft^2);

> M[w]:=16.0426*lb[m]/mol;

The power required by the compressor is found by multiplying the work by the mass flow rate, which is given by r₁vA.

> power:=evalf(-W*v1*Pi*d^2*p1*M[w]/4/R/T2);

If we now convert the answer to units of horsepower, we obtain very close to the book’s answer of 504 hp.

> power:=power*(hp/(550*ft*lb[f]/sec));