Lambert's Law:

> q[b,theta]:=q[b]/Pi*cos(theta);

> q[b]:=sigma*T^4;

> q[b,theta];

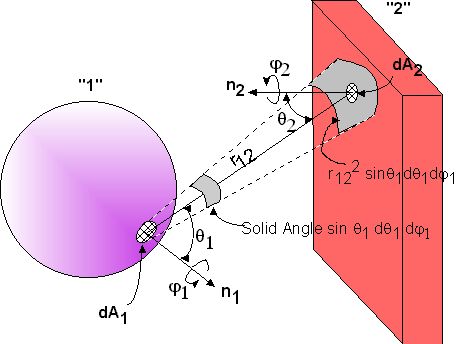
Now consider the diagram shown in figure 1. In order to find the energy transferred between the two, a line r12 was created between the two surfaces. The angles theta1 and theta2 are the angles between r12 and the normal lines to the surfaces. Phi1 and Phi2 are measures of the rotation in the third dimension. Lambert's law applied to this case gives the following as the energy radiated by body 1 in a given amount of time:

> E:=sigma*T[1]^4/Pi*cos(theta[1])*dA[1]*sin(theta[1])*d(theta[1])*d(phi[1]);

Also as shown in the diagram, not all of the energy radiating from body 1 will be received by body 2. In order to account for this, the following is the ratio of the area of dA2 projected on a plane perpendicular to r12 to the area formed by the intersection of the solid angle sin(theta1)*d(theta1)*d(phi1) with a sphere of radius r12 with a center at dA1.

> ratio:=dA[2]*cos(theta[2])/(r[12]^2*sin(theta[1])*d(theta[1])*d(phi[1]));

By multiplying these two expressions, we get the differential for the total energy transferred from 1 to 2.

> dQ[12]:=E*ratio;

The same method can be applied for the reverse direction, but it can easily be seen that the only difference will be in the Temperature term.

> dQ[21]:=subs(T[1]=T[2],dQ[12]);

The net rate of energy transfer, then, is just the difference in energy transfers.

> dQ:=dQ[12]-dQ[21];

> simplify(dQ);

Next we integrate both sides to get the total heat transfer (but first we have to divide dQ by dA1*dA2 since Maple's "int" program requires the variables of integration to be entered separately):

> Q:=int(int(dQ/(dA[1]*dA[2]), A[1]), A[2]);

> simplify(Q);

BSL simplifies this further with the introduction of functions F12 and F21, where:

> F[12]:=1/(Pi*A[1])*int(int(cos(theta[1])*cos(theta[2])/r[12]^2, A[1]), A[2]);

> F[21]:=1/(Pi*A[2])*int(int(cos(theta[1])*cos(theta[2])/r[12]^2, A[1]), A[2]);

By placing F12 into the equation given by BSL, we see that it is the same as the one given for Q above

> A[1]*F[12]*sigma*(T[1]^4-T[2]^4);

The reason for adding the view factor F12 is because it is the actual portion of radiation emitted by A1 that is absorbed by A2. Calculating view factors, though, is difficult. Hottel and company calculated some view factors, and is results for the radiation between rectangles in perpendicular planes can be found in BSL, p. 441.

>

What we have done so far dealt with just two surfaces. Now we will expand that to a set of surfaces that makes a complete enclosure (like the inside of a box). It is easy to generalize the equation for Q by using the view factor.

> Q[is]:=sigma*A[i]*sum(F[ij]*(T[i]^4-T[j]^4), j=1...n);

> eq:=sum(F[ij], j=1...n)=1; This is true because in a closed space, all the radiation that leaves a surface must be absorbed by some surface.

It would look like this:

> sum(F[ij], j=1...n):=1;

Rearranging, we could say:

> n:=1/F[ij];

we can see then that the n*Fij, which equals 1, would drop out of the equation above. The final answer would look similar to this (except that there is no need to change n to 1/Fij in the sum):

> Q[is];

Which matches eqn. 14.4-13 from BSL.