Now we will compare the results of our calculations for the three fins. First we present a table of the values for the preferred length, height, and profile area.
|
Profile |
| Dimension | Minimal | Rectangular | Triangular | |
| L | 2 | 1.5956 | 1.6844 | * 1 / (h) * (Qtot / q0) |
| y0 | 2 | 1.2640 | 1.6549 | * 1 / (h*k) * (Qtot / q0)2 |
| Area | (4/3) = 1.333..... | 2.0169 | 1.3939 | * 1 / (h2*k) * (Qtot / q0)3 |
| qL/q0 | 0 | 0.4570 | 0.27735 |
We can see from this table that fins with a rectangular profile require almost 50% more material than those of a minimal or triangular profile. Although the minimal one is the most efficient, we can see that with the triangular fin we get an area that is almost as economical as the minimal profile one. This of course requires the entire fin to operate at a very temperature excess throughout the fin.
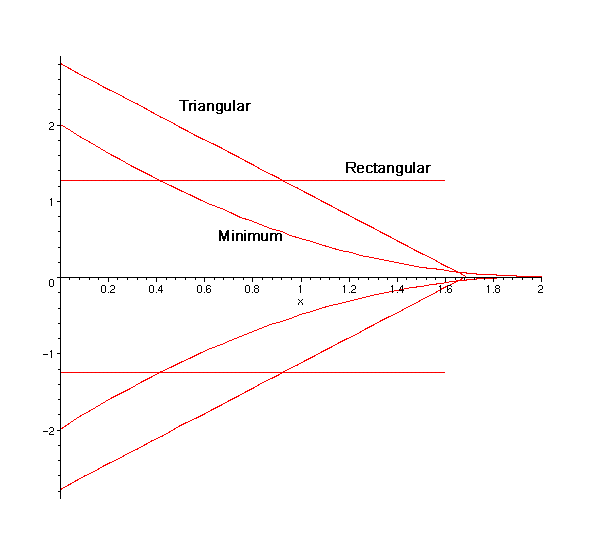
First we plot the three fins to get a quick comparison of their
relative sizes. We will assume that they all have the same value for h, (qtot
/ q0), and k.
So all three of these fins radiate the same amount of heat, and this is the
shape necessary to do it.
> y_min:=x->-2*x+x^2/2+2:
> y_tri:=x->1.654987627*(1.684497599-x):
> y_rect:=x->1.264066295:
>
>
with(plots):
p1:=plot(y_min(x),x=0..2):
p2:=plot(y_tri(x),x=0..1.684497599):
p3:=plot(y_rect(x),x=0..1.595642608):
p4:=plot(-y_min(x),x=0..2):
p5:=plot(-y_tri(x),x=0..1.684497599):
p6:=plot(-y_rect(x),x=0..1.595642608):
display(p1,p2,p3,p4,p5,p6);

>
Now we will do a quick numerical example comparing Copper, Aluminum, and Iron for these fins. The calculations below are summarized here in this table.
| Metal | k in BTU/hr/ft/F | r in lb/ft3 | Vol / Vol of Copper | Weight / Weight of Copper |
| Copper | 222 | 556 | 1 | 1 |
| Aluminum | 121 | 169 | 1.83 | 0.557 |
| Iron | 30 | 487 | 7.40 | 6.48 |
This table shows that copper fins require the smallest volume and aluminum requires the least weight for a fin to distribute the same total heat and starting temperature. The h for each is assumed to be constant since it can be changed just as a function of the smoothness of a the fin. Iron is obviously the least favorable as it is the highest in volume and weight to do the same job as a Copper or Aluminum one would do..
>
k_Cu:=222*BTU/hr/ft/F;
k_Al:=121*BTU/hr/ft/F;
k_Fe:=30*BTU/hr/ft/F;
![]()
![]()
![]()
>
rho_Cu:=556*lb/ft^3;
rho_Al:=169*lb/ft^3;
rho_Fe:=487*lb/ft^3;
![[Maple Math]](images/proj95.gif)
![[Maple Math]](images/proj96.gif)
![[Maple Math]](images/proj97.gif)
> area_min:=k->4/3*1/(h^2*k):
>
>
Vol_Cu_min:=Z*area_min(k_Cu):
Vol_Al_min:=Z*area_min(k_Al):
Vol_Fe_min:=Z*area_min(k_Fe):
>
W_Cu_min:=Vol_Cu_min*rho_Cu:
W_Al_min:=Vol_Al_min*rho_Al:
W_Fe_min:=Vol_Fe_min*rho_Fe:
>
evalf(Vol_Cu_min/Vol_Cu_min);
evalf(Vol_Al_min/Vol_Cu_min);
evalf(Vol_Fe_min/Vol_Cu_min);
![]()
![]()
![]()
>
evalf(W_Cu_min/W_Cu_min);
evalf(W_Al_min/W_Cu_min);
evalf(W_Fe_min/W_Cu_min);
![]()
![]()
![]()