The Straight Fins of Triangular Profile

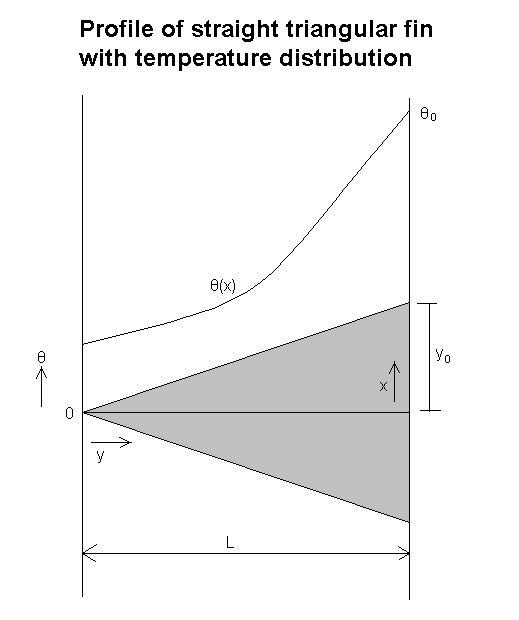
Lastly we will calculate the fin of a triangular profile, or that of a wedge.  It is possible to reduce this to that of a wedge, but the equations are beyond the scope of this project.  Further information on wedge shaped fins can be found in a paper published by D.R Harper and W.B.Brown in the 1922 National Advisory Committee on Aeronautical Technology Report #158, on page 677.

> restart;

Start with Newton's equation of cooling as always.

> q:=(y,x)->-k*y(x)*diff(theta(x),x);
eqn1:=-diff(q(y,x),x)=h*theta(x):
eqn2:=simplify(eqn1/k);

Here we substitute our equation of a line.  It is important to note here that the diagram above is NOT backwards.  We just made a small convention to put the heat source at x=L and the tip of the fin at x=0.  Thus this will simplify our profile equation to the one shown below.

The solution involves a complicated Bessel function of the first kind.

> s:=dsolve({eqn1,theta(0)=C1},theta(x));
assign(s):

> theta:=unapply(theta(x),x):

We have the initial condition knowing the temperature at x=L.

> C1:=solve(theta[0]=theta(L),C1):
theta(x);

Now we calculate the total heat across the bar.

> qtot:=h*int(theta(x),x):

> qtot:=eval(qtot,x=L)-eval(qtot,x=0);

The equation for profile area.

> eqn3:=Area=L*y0/2:
L:=solve(eqn3,L):

However, we need to take a derivative with respect to y0, so we will need to substitute back in to get a y0.

> eqn11:=u=4*sqrt(h/k)*Area*y0^(-3/2):
solve(eqn11,y0):
y0:=%[1];

> simplify(eqn4,assume=positive);

Here we take the derivative to find the maximum value for total heat / initial temperature excess.

> eqn6:=simplify(diff(eqn4/theta[0],u),assume=positive);

> eqn7:=simplify(eqn6*u^(4/3)*BesselI(0,u)^2*3/2^(2/3)/k^(1/3)/Area^(1/3)/h^(2/3));

Use a numerical solver because Maple cannot come up with a closed form answer due to the Bessel functions.

> u:=fsolve(eqn7=0,u,1..3);

Now that we have our most favorable u, we will use that to generate the characteristic length, height, and profile area.

> unassign('y0','L');

> Area:=L*y0/2:

> eqn11:
y0:=solve(eqn11,y0);

> eqn12:=simplify(Qtot/theta[0]=eqn4/theta[0],assume=positive);

> L_eqn:=solve(eqn12,L);

> unassign('y0','Area'):

> eqn13:=algsubs(y0=Area*2/L,eqn4):

> Area:=L*y0/2:
L:=solve(eqn11,L):

> eqn14:=Qtot=eqn13:

> y0_eqn:=solve(eqn14,y0);

> Area_eqn:=L_eqn*y0_eqn/2;

Here we see that although a lot of heat is lost, the temperature of the fin as a whole is still quite high at the end.

> n:=simplify(theta(0)/theta(L),assume=positive);