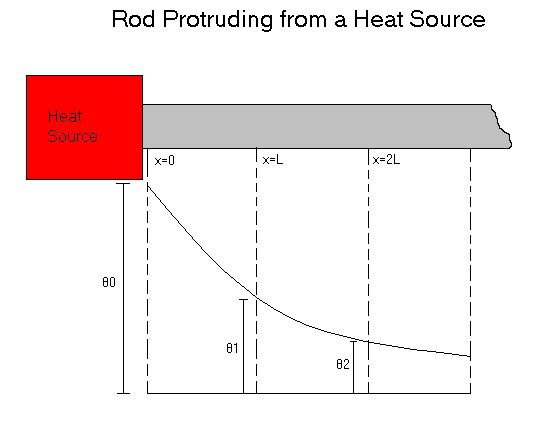
Since our previous work would give no accurate results with rods of a "not very long" length, we need to make an adjustment. We will now calculate the relative k's by the measurement of differences between 3 spots on the rod. For simplicity we will make the three spots of equal distance.
We take our general equation from the previous section.
> Theta:=x->M*exp(-m*x)+N*exp(m*x);
![[Maple Math]](images/proj21.gif){kind=small}
...and evaluate it at the three locations, 0,L, & 2L
>
eqn:=Theta(0)+Theta(2*L);
eqn2:=Theta(L);
![[Maple Math]](images/proj22.gif){kind=small}
![[Maple Math]](images/proj23.gif){kind=small}
For simplicity we replace (Theta(0) + Theta(2))/2*Theta(1) = n
> eqn3:=n=eqn/(2*eqn2);
![[Maple Math]](images/proj24.gif)
> eqn3:=simplify(eqn3, assume=positive);
![[Maple Math]](images/proj25.gif){kind=small}
>
solve(eqn3,L):
f:=unapply(%[1]*m,n);
![[Maple Math]](images/proj26.gif){kind=small}
Now we have a dimensionless equation for the temperature differences.
> eqn4:=m[1]/m[2]=f(n[1])/f(n[2]);
![[Maple Math]](images/proj27.gif)
Substitute back in for our m's.
>
m[1]:=sqrt(h[1]*C/(k[1]*SA)):
m[2]:=sqrt(h[2]*C/(k[2]*SA)):
Solve the equations to get a relationship for the ratio of the thermal conducitivities.
>
eqn4:=simplify(eqn4, assume=positive):
eqn5:=k1/k2=solve(eqn4,k[1])/k[2];
![[Maple Math]](images/proj28.gif)
We can see here that if the surface conductivities are made to be equal, then we can get relative heat differences by just measuring the temperatures at three points on two rods and comparing the differences. Now the length of the rod is not factor.