Temperature Profile of Example 15.4-2

Parallel or Counter-Flow Heat Exchangers

Refer to Figure 15.4-2

If the flows of both the streams are positive, we have a parallel exchanger

> restart;

> eqh:=wCph*D(Th)(z)=U0*2*Pi*r0*(Tc(z)-Th(z)); Balance on the hot side: a combination of eq. 15.4-10 and eq. 13.1-8.

> eqc:=-wCpc*D(Tc)(z)=U0*2*Pi*r0*(Tc(z)-Th(z)); Just like eqh, but for the cold side.

> s:=dsolve({eqh,eqc,Tc(0)=Tc1,Th(0)=Th1},{Tc(z),Th(z)});

> assign(s); Th:=unapply(Th(z),z);Tc:=unapply(Tc(z),z);

> Tc1:=85; Tc2:=120; Th1:=200; wCpc:=5000; wCph:=10000.; r0:=(.5/12); U0:=80; This is one set of parameters that are commonly specified for a heat exchanger.

> plot({Th(z),Tc(z)},z=0...100.,color=[red,blue]);

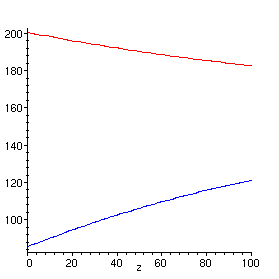
This is typical parallel flow. It is not an efficient way to operate.

> evalf(Tc(100));

> Tc1:=120; Tc2:=85; wCpc:=-5000; As in the parallel flow case.

Now our flow will be in the opposite direction to z for the hot stream.

> plot({Th(z),Tc(z)},z=0...100,color=[red,blue]);

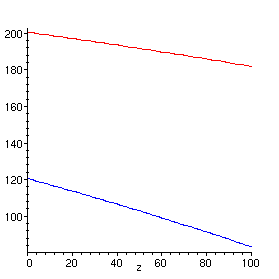
This is the temperature profile for the counter-current flow case. It is more effecient, as is illustrated by the required water flow rate in our the sample problem.