Setting up the problem

We have a case of unsteady heat conduction in a solid. The equation of energy for spherical coordinates simplifies greatly because the body is a solid. We can therefore ignore all of the terms including velocities or viscosity. In addition, by symmetry we assume the temperature varies only with time and radial position. Using these assumptions, equation 10.2-3C yields . In this equation, is the density, C_p is the heat capacity, and k is the thermal conductivity. Additionally, by assuming the thermal conductivity is independent of temperature or position, we can define the thermal diffusivity of the solid, . Using this definition, we write the above equation as .

By conservation of energy, we can also find another equation relating the heat flux from the sphere to the heat diffused in the liquid. The heat diffused in the fluid is simply . The heat flux through the surface of the sphere is , where SA is the surface area of the sphere. Using Table 10.2-1, we can write . Also, since we are dealing with a sphere we can write , where V_s is the volume of the sphere. Using the definition of thermal diffusivity, we also have . The heat flux through the surface of the sphere is therefore . Equating the fluid and solid, we find. Following the book’s example, we define a new dimensionless variable, . 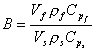Utilizing this definition, the equation can be simplified to .

The boundary conditions for this problem are: At time 0 the temperatures of the solid and fluid are at their initial values, the continuity of temperature is maintained at the boundary between the two bodies at all times, and the temperature of the center of the solid is finite at all times. Next we will use Maple to transform these equations into dimensionless variables.