Page by: Jennifer Fletcher and Star Chacko
Table of Contents:
1. Example Problem 2.3-2
2. Solution to Ex. 2.3-2
3. Extra work including heat transfer
through circular tube
A fluid that is very nearly described by the Bingham model is flowing through a vertical tube as the result of a pressure gradient and/or gravitational acceleration.

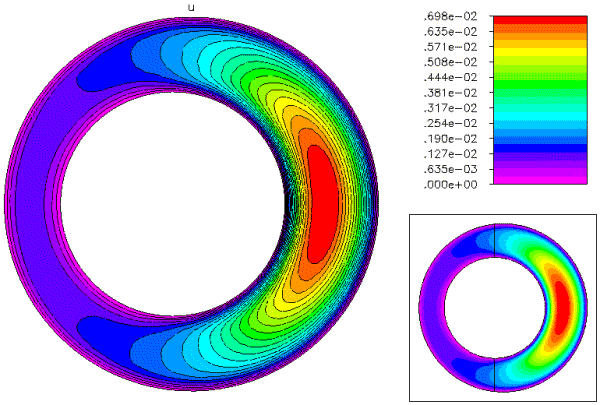
Buoyancy driven flows of two Bingham fluids in an inclined duct are considered, providing a simplified model for many oil-field cementing processes. The flows studied are near-uniaxial and stratified, with the heavy fluid moving down the incline, displacing the lighter fluid upwards. Flow of two Bingham fluids in a cylindrical duct: heavier fluid (cement) flows downwards in axial direction. Lighter fluid (mud) is below the cement. These calculations were implemented with PLTMG. (References: Ian Frigaard, Otmar Scherzer )
The radius and length of the tube are R and L. respectively. It is desired to obtain a relation between the volume rate of flow Q and the combined pressure and gravity forces acting on the fluid.
The momentum flux distribution for flow of any kind of fluid through a circular tube is given by the following equation:
![]()
According to Figure 1.2-1 in the text, for a Bingham
fluid the velocity gradient is zero when the momentum flux is less than
the value ![]() . Hence one expects
a "plug flow" region in the central part of the tube as shown in the figure
below:
. Hence one expects
a "plug flow" region in the central part of the tube as shown in the figure
below:
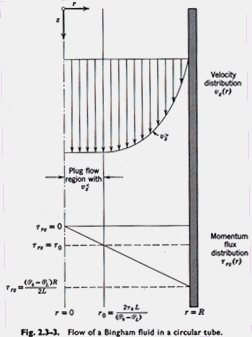
Outside the plug-flow region the momentum flux and the velocity gradient are related according to Eq. 1.2-2a in the text. Substitution of the cylindrical coordinate version of Eq. 1.2-2a into Eq. 2.3-12 yields:
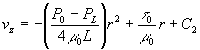
The constant C2 is evaluated by making use of the boundary condition that is vz=0 at r=R. Then the velocity distribution becomes finally
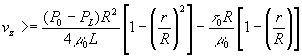 r>=r0
r>=r0
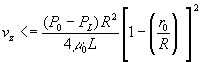 r<
r0
r<
r0
Here r0 is the radius of the plug-flow region, defined by t0=(P0-PL)r0/2L. The latter equation above is obtained by setting r=r0 in the former equation above and simplifying.
The volume rate of flow may be calculated from
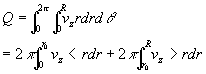
The expressions for vz < and vz > may be inserted and the integrals evaluated. Less algebra is required, however, if one integrates the first expression for Q by parts:
![]()
The quantity r2vz is zero at both limits, and in the integral the lower limit may be replaced by r0 because dvz/dr=0 for r<=r0.
Hence the volume rate of flow is, if tR>t0
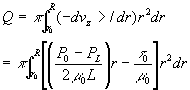
By performing the integration and using the symbol tR
for the momentum flux at the wall, ![]() ,
one obtains when tR>t0:
,
one obtains when tR>t0:
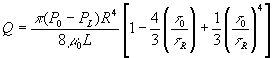
which is known as the Buckingham-Reiner Equation. When t0 is zero, the Bingham model reduces to the Newtonian model and the final equation presented above reduces appropriately to the Hagen-Poiseuille equation.
(References: Bernard Spang)
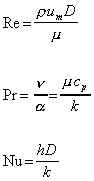
All properties at fluid bulk mean temperature (arithmetic mean of inlet and outlet temperature).
Nusselt numbers Nu0 from sections 1-1 to 1-3 have to be corrected for temperature-dependent fluid properties according to section 1-4.
1-1 Thermally developing, hydrodynamically developed laminar flow (Re < 2300)
Constant wall temperature:
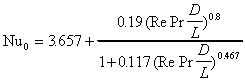 (Hausen)
(Hausen)
Constant wall heat flux:
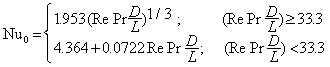 (Shah)
(Shah)
1-2 Simultaneously developing laminar flow (Re < 2300)
Constant wall temperature:
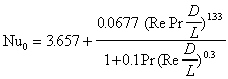 (Stephan)
(Stephan)
Constant wall heat flux:
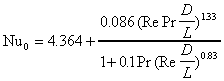
which is valid over the range 0.7 < Pr < 7 or if Re Pr D/L < 33 also for Pr > 7.
1-3 Fully developed turbulent and transition flow (Re > 2300)
Constant wall heat flux:
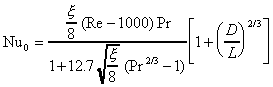 (Petukhov,
Gnielinski)
(Petukhov,
Gnielinski)
where
![]()
Constant wall temperature:
For fluids with Pr > 0.7 correlation for constant wall heat flux can be used with negligible error.
1-4 Effects of property variation with temperature
Liquids, laminar and turbulent flow:
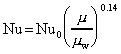
Subscript w: at wall temperature, without subscript: at mean fluid temperature
Gases, laminar flow:
Nu = Nu0
Gases, turbulent flow:
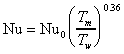
(Temperatures in Kelvin )