by Greg Johnson
(Picture courtesy of Erin Chang)
by Greg Johnson

(Picture courtesy of Erin Chang)
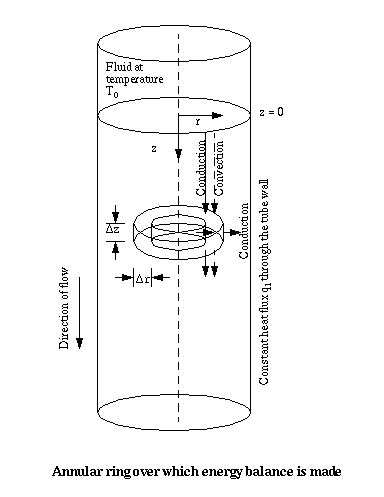
A steady-state forced convection heat transfer problem is encountered when considering a viscous fluid with constant physical properties (density, viscosity, thermal conductivity, heat capacity) in laminar flow in a cylindrical tube of radius R. The fluid, originally at a temperature T0, is subjected to a constant wall heat flux, q1. Heat transfer occurs by convection in the axial direction and by conduction in the axial and radial directions. Through a thermal energy balance over a ring-shaped element, it is seen that the system can be modeled by a partial differential equation:
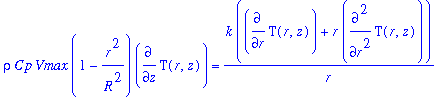 (1)
(1)
with boundary conditions:
1) at r=0 T=finite
2) at r=R -k(dT/dr)=q1
(a constant)
3) at z=0 T=T0
The problem can be simplified by expressing the PDE (equation (1)) in terms of the diminsionless quantities:
![]() (2)
(2)
![]() (3)
(3)
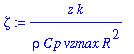 (4)
(4)
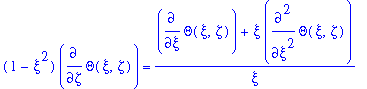 (5)
(5)
We assume the solution to this equation will be of the form:
![]() (6)
(6)
where Thetainfinity is the limiting form of the solution for large values of zeta. The limiting form is solved in BS&L Section 9.8 and turns out to be:
![]() (7)
(7)
To solve for Thetad, which
physically represents the temperature profile for small values of zeta
and should be damped exponentially with increasing zeta, we attempt to
solve the PDE given in equation (5) subject to the following set of boundary
conditions:
1) at xi=0 d(Thetad)/d(xi)=0
2) at xi=1 d(Thetad)/d(xi)=0
3) at zeta=0 Thetad=Thetainfinity(xi,0)
To attempt to solve the equation we assume a product solution of two functions of single variables (X(xi) and Z(zeta)):
Thetad(xi,zeta)=X(xi)Z(zeta) (8)
From this assumption we can rewrite the PDE in equation (5) as two ordinary differential equations and can also redefine the set of boundary conditions:
from (6), d(Thetad)/d(xi)=X'Z and d(Thetad)/d(zeta)=XZ'
so rewriting equation (5) gives:
Taking the Z and zeta terms to the right hand side and the X and xi terms to the left hand side yields:
Z'/Z = (xi(1-xi2)X)-1(X'+xi(X'')) = -c2 (10)
Equation (8) equates the two expressions to a separation constant (-c2), from which we can turn the PDE in (8) to two ODE's as such:
Z'/Z = -c2 (11) (xi(1-xi2)X)-1(X+xi(X'')) = -c2 (12)
Equation (12) can be rearranged:
X+xi(X'') = -c2 (xi(1-xi2)X)
X+xi(X'') + c2(1-xi2)X) = 0 (13)
Knowledge of the product rule of differential calculus reveals that Equation (13) can be rewritten with the differential operator (d/d(xi)):
(1/xi)(d/d(xi))[xi(X')] + c2((1-xi2)X) = 0 (14)
The form of the ODE expressed in Equation (14) agrees with equation 11.2-7 in BS&L. Now our system is modeled by two ODEs (Equations (11) and (14)) which are more readily solved than PDEs. An analytical solution to Equation (11) is found very easily.
![]() (15)
(15)
Unfortunately, the analysis of the 2nd ODE (Equation (14)) isn't as simple. Analytical solutions to the equation are much more difficult to obtain for X(xi) as defined in Equation (14). However, the situation can be simplified by recognizing the form of the problem as a Sturm-Liouville type. A Sturm-Liouville problem is a boundary value problem in which sets of corresponding characteristic functions are orthogonal with respect to a weighting function. The differential equation takes the form:
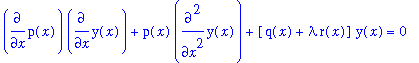 (16)
(16)
where the weighting function is given by r(x). Comparing Equation (14) to (16), it is seen that if p(x)=xi, q(x)=0, lambda = -c2 and r(x)=xi(1-xi2) (-NOTE-This is the form of the weighting function that will come up later) , the forms are identical. A Sturm-Liouville problem must also contain two homogeneous boundary conditions. Rewriting the boundary conditions with respect to our assumed product solution (Equation(8)) yields:
1) at xi = 0 dX/d(xi) = 0
2) at xi = 1 dX/d(xi) = 0
3) at zeta = 0 Thetad=Thetainfinity(xi,0)
We recognize conditions 1 and 2 as homogeneous thus the second ODE of our system (given in Equation 15) is, in fact, of Sturm-Liouville type. From the characteristics of this type of problem, there will be an infinite number of functions satisfying Equation (14), so we can rewrite our product solution for Equation (8) using our newly discovered information and Equation (15):
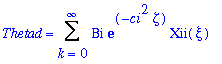 (17)
(17)
Where Bi is a conglomerate of integration constants multiplied together (_C1 from Equation (15) is a factor of B). Upon combination with Equation (6):
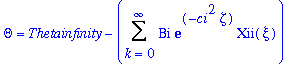 (18)
(18)
Which agrees with Equation 11.2-8 in BS&L. The boundary conditions define the interval in the problem to be xi=[0,1] (physically this definition implies the circular cross-section of the pipe) thus the infinite set of characteristic solutions to the ODE (Equation (14)) will be orthogonal on this interval with respect to a weighting function r(xi). By definition, this implies that the integral of the product of any two of these solutions will vanish on the interval from 0 to 1:
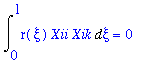 (19)
(19)
Where i and k are indicies of two solutions to Equation (14) and where i is not equal to k. Now, taking the third boundary condition (at zeta=0, Thetad = Thetainfinity(xi,0) ) and combining it with Equation (17):
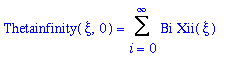 (20)
(20)
Multiplying both sides of the equation
by [r(xi)Xik(xi)] yields:
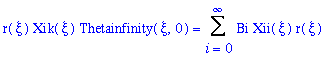 (21)
(21)
Integrating Equation (22) with respect to xi for xi=[0,1] would appear to yield a very complicated expression with very little functionality. However from the orthoganality definition worked out earlier and expressed in Equation (19), all the terms on the right hand side of the equation will dissappear except for the singular case when i=k. Thus:
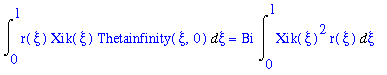 (22)
(22)
Remembering the version of the weighting function r(xi) resulting from the preceding discourse:
![]() (23)
(23)
From which the constant B can be found for any solution to Equation (15) (here given the index k):
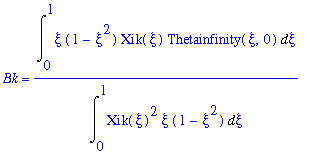 (24)
(24)
Equation (24) is consistent with Equation 11.2-9 in BS&L and combined with (18) these monsters would give the complete answer. However, it has been assumed that the Xik(xi) characteristic functions could be found for all values of k and this is not neccessarily true. Bird points out that the solution has been found using numerical methods by Siegel, Sparrow and Halmann for values only less than eight. Using Maple to try to solve the ODE in Equation (14) does give a general answer in terms of Whittaker functions and imposing the first boundary condition solves for the first integration constant. However, the impsoition of the second boundary condition gives problems as the denominator repeatedly turns out to be zero. BS&L notes that in Sparrow, Siegel and Halmann's treatment of the problem they applied the boundary condition at xi=1 and then went on to solve for c. Maple can try to do this but it leads to the introduction of some wierd stuff.