
Section 1.4
Theory of Viscosity of Gases at Low Density
Spring 2000 Project by Kristin Clopton
The viscosity (in units of g/cm/s) of a pure monatomic gas is predicted by Chapman-Enskog theory, and is given by Equation 1.4-18 in BS&L as:

where: T is the absolute temperature in K
M is the molecular weight in g/mol
sigma is a Lennard-Jones parameter in Angstroms (given in Table
B-1)
Omegamu is a dimensionless function of (KT/epsilon) (given
in Table B-2)
Chapman-Enskog theory has been further extended to include multicomponent gas mixtures - and generally the formula of Wilke is used. Equations 1.4-19 and 1.4-20 in BS&L describe this:
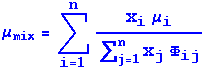
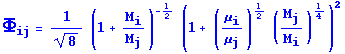
where: n is the number of chemical
species
xi and xj are mole fractions of two species
mui and muj are viscosities of two species in g/cm/s at the
specified temperature and pressure
Mi and Mj are the molecular weights of two species in g/mol
When solving problems involving the prediction of viscosity, whether for a single gas or a mixture, both Matlab and Maple can be used.
*In Matlab, two useful programs exist - mucalc and mixmu. The first step in using either of these programs is to run a start301 to set property data. Mucalc takes arguments of temperature and the index number of the gas, and returns viscosity in units of kg/m/s. Mixmu takes arguments of the mole fraction of each compound in a gas mixture, temperature, and the indices of the compounds, and returns viscosity of the entire mixture in units of kg/m/s. (NOTE: These units differ from those used in BS&L - those are g/cm/s!)
*In Maple, Equations 1.4-18, 19,
& 20 can be manipulated in a worksheet to give very similar
answers to those found by Matlab.
Example 1.4-2
Prediction of the Viscosity of a Gas Mixture at
Low Density
Question:
Predict the viscosity of the following gas mixture
at 1 atm and 293 K from the given data on the pure components at
1 atm and 293 K. Given mole fractions, molecular weights,
and viscosities for CO2, O2, and N2. Mole fractions for
respective species: 0.133, 0.039, 0.828. Molecular weights
for respective species: 44.010, 32, 28.016 in g/mol.
Viscosities: 1462e-7, 2031e-7, 1754e-7 in g/cm/s.
Answer:
- The easy route....use mixmu in Matlab! Ta-da...answer in 2 seconds!
- The slightly more painful (but very instructive!) route.... use Maple and Equations 1.4-19 & 20:
So, in Maple, we start out...
| Indices for the 3 compounds will be: | 1 corresponds to CO2 |
| 2 corresponds to O2 | |
| 3 corresponds to N2 |
> restart;
Mole fractions of each species:
> x[1]:=0.133; x[2]:=0.039; x[3]:=0.828;
![]()
![]()
![]()
Molecular weights of each species:
> M[1]:=44.010*g/mol; M[2]:=32.000*g/mol; M[3]:=28.016*g/mol;
![]()
![]()
![]()
Viscosities of species (we could use BS&L values given in the problem, or...calculate them ourselves):
- Calculate in Matlab using a start301 and mucalc
- or -
- Calculate in Maple using Equation 1.4-18 and Tables B-1 & B-2
> mu[1]:=.1464707550e-3*g/cm/s; mu[2]:=.2028770331e-3*g/cm/s; mu[3]:=.1746432201e-3*g/cm/s;
![]()
![]()
![]()
Now that we have the viscosity of each species, we can calculate that of the mixture making by making use of Equations 1.4-19 & 20. The strategy is to use Equation 1.4-20 and calculate Phi(ij) for each possible combination of species. Then these values will be combined as prescribed in Equation 1.4-19.
Let's begin with species 1 - CO2:
(We know that since Phi(ij) is dimensionless, any combination such that i=j will simply give 1.)
> Phi11:=1;
![]()
Phi for CO2 with O2
> Phi12:=(1/sqrt(8))*((1+(M[1]/M[2]))^(-.5))*(1+((mu[1]/mu[2])^.5)*((M[2]/M[1])^.25))^2;
![]()
Phi for CO2 with N2
> Phi13:=(1/sqrt(8))*((1+(M[1]/M[3]))^(-.5))*(1+((mu[1]/mu[3])^.5)*((M[3]/M[1])^.25))^2;
![]()
Once we have the Phi's for these combinations, we can proceed with Eqn 1.4-19. A convient first step is to compute the inside of the summation on the bottom - just multiply each of our Phi's by the corresponding mole fraction.
> x1Phi11:=x[1]*Phi11;
![]()
> x2Phi12:=x[2]*Phi12;
![]()
> x3Phi13:=x[3]*Phi13;
![]()
Now we can take this summation for n = 1 (i.e. CO2).
> denominator[1]:=simplify(x1Phi11+x2Phi12+x3Phi13);
![]()
Now we repeat this process for the two remaining species...
For species 2 - O2:
Phi for O2 with CO2
> Phi21:=(1/sqrt(8))*((1+(M[2]/M[1]))^(-.5))*(1+((mu[2]/mu[1])^.5)*((M[1]/M[2])^.25))^2;
![]()
Phi for O2 with itself gives unity
> Phi22:=1;
![]()
Phi for O2 with N2
> Phi23:=(1/sqrt(8))*((1+(M[2]/M[3]))^(-.5))*(1+((mu[2]/mu[3])^.5)*((M[3]/M[2])^.25))^2;
![]()
Multiplication by the mole fractions
> x1Phi21:=x[1]*Phi21;
![]()
> x2Phi22:=x[2]*Phi22;
![]()
> x3Phi23:=x[3]*Phi23;
![]()
Summation for n =2 (i.e. O2)
> denominator[2]:=simplify(x1Phi21+x2Phi22+x3Phi23);
![]()
For species 3 - N2:
Phi for N2 with CO2
> Phi31:=(1/sqrt(8))*((1+(M[3]/M[1]))^(-.5))*(1+((mu[3]/mu[1])^.5)*((M[1]/M[3])^.25))^2;
![]()
Phi for N2 with O2
> Phi32:=(1/sqrt(8))*((1+(M[3]/M[2]))^(-.5))*(1+((mu[3]/mu[2])^.5)*((M[2]/M[3])^.25))^2;
![]()
Phi for N2 with self is unity
> Phi33:=1;
![]()
Multiplication by mole fractions
> x1Phi31:=x[1]*Phi31;
![]()
> x2Phi32:=x[2]*Phi32;
![]()
> x3Phi33:=x[3]*Phi33;
![]()
Summation for n = 3 (i.e. N2)
> denominator[3]:=simplify(x1Phi31+x2Phi32+x3Phi33);
![]()
With all of the denominators calculated, we now just need the numerators. With a loop over all 3 species, we calculate these as per the formula:
> for i from 1 to 3 do numerator[i]:=x[i]*mu[i]; od;
![]()
![]()
![]()
With a similar loop over the 3 species, we now divide the numerator of each by the denominators:
> for i from 1 to 3 do mu[i]:=numerator[i]/denominator[i]; od;
![]()
![]()
![]()
Finally, we can take the larger summation of all of these to produce the viscosity of the mixture:
> mu[mix]:=sum('mu[i]','i=1..3');
![]()
This answer is fairly close to that calculated in BS&L of 1714e-7 g/cm/s.