ch4_2b.html

ch4_2b.mw

Session 4.2 Defining and solving Differential Equations Part b Two ODEs

> restart;

We want to solve two differential equations simultaneously:

dx1/dt = -x1 + ax2 ; x1(0) = 1

dx2/dt = bx1 - 2x2 ; x2(0) = 0

a and b are constants

> de1:=D(x1)(t)=-x1(t)+a*x2(t);The operator notation for differentiation is somewhat more concise than diff.

> de2:=D(x2)(t)=b*x1(t)-2*x2(t);

> ic1:=x1(0)=1;

> ic2:=x2(0)=0;

> s1:=dsolve({de1,de2,ic1,ic2},{x1(t),x2(t)});

The differential equations and initial conditions are all listed in the first set of braces.

The variables to be found are listed in the second set of braces.

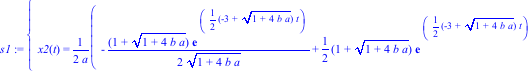
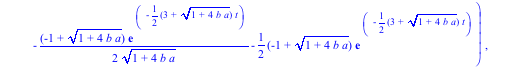
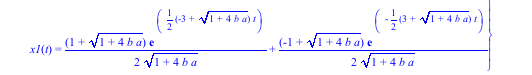
$s1 := {x2(t) = 1/2*(-1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2)+1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)-1/2*(-1+(1+4*b*a)^(1/2))*exp(-1/2*(3+(1+4*b*a)^(1/2...$ $s1 := {x2(t) = 1/2*(-1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2)+1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)-1/2*(-1+(1+4*b*a)^(1/2))*exp(-1/2*(3+(1+4*b*a)^(1/2...$ $s1 := {x2(t) = 1/2*(-1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2)+1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)-1/2*(-1+(1+4*b*a)^(1/2))*exp(-1/2*(3+(1+4*b*a)^(1/2...$

We can also solve this equation using a Laplace Transform:

> s2:=dsolve({de1,de2,ic1,ic2},{x1(t),x2(t)},laplace);

Note the addition of the term "laplace" at the end of the command

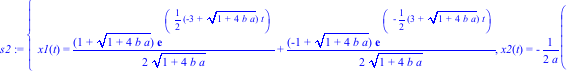
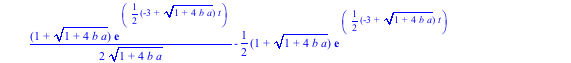
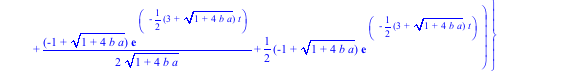
$s2 := {x1(t) = 1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2)+1/2*(-1+(1+4*b*a)^(1/2))*exp(-1/2*(3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2), x2(t) = -1/2*(1/2*(1+(1+4*b*a)^(1/2))*e...$ $s2 := {x1(t) = 1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2)+1/2*(-1+(1+4*b*a)^(1/2))*exp(-1/2*(3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2), x2(t) = -1/2*(1/2*(1+(1+4*b*a)^(1/2))*e...$ $s2 := {x1(t) = 1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2)+1/2*(-1+(1+4*b*a)^(1/2))*exp(-1/2*(3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2), x2(t) = -1/2*(1/2*(1+(1+4*b*a)^(1/2))*e...$

> assign(s1);x1:=unapply(x1(t),t);x2:=unapply(x2(t),t);

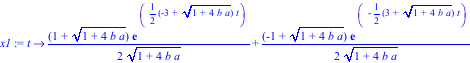
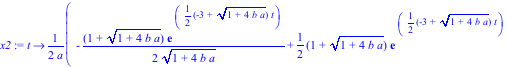
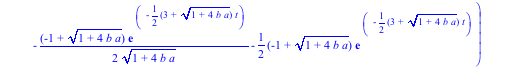
x2 := proc (t) options operator, arrow; 1/2*(-1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)/(1+4*b*a)^(1/2)+1/2*(1+(1+4*b*a)^(1/2))*exp(1/2*(-3+(1+4*b*a)^(1/2))*t)-1/2*(-1+(1+4*b*a)^(1/2))*e...

> x1(0);x2(0);

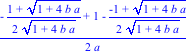
1/2*(-1/2*(1+(1+4*b*a)^(1/2))/(1+4*b*a)^(1/2)+1-1/2*(-1+(1+4*b*a)^(1/2))/(1+4*b*a)^(1/2))/a

> simplify(x1(0));simplify(x2(0));