Look for this session in /home/ceng303/maple/sessions as: ch1_8.mw

Session 1.8: Integrals of expressions and functions

> restart;

>fe1:=sin(x); Expression giving a function of x

fe1 := sin(x)

>f:=x->x^2-2*cos(x); Mapping function of single variable

f := proc (x) options operator, arrow; x^2-2*cos(x) end proc

>int(fe1,x); Integral of sin(x)

-cos(x)

>int(f(t),t); Integral of defined function

1/3*t^3-2*sin(t)

>int(fe1,x=0...3); Define limits of integration

-cos(3)+1

>evalf(%); Evaluate answer.  Note : % is used to insert the last result instead of typing in the answer

1.989992497

> int(f(x),x);

1/3*x^3-2*sin(x)

> int(f(x),x=-1...1);

-4*sin(1)+2/3

> int(f(x)*sin(x),x);

-x^2*cos(x)+2*cos(x)+2*x*sin(x)+cos(x)^2

>sin(x)/f(x); Complicated function

sin(x)/(x^2-2*cos(x))

>int(%,x); Maple cannot always calculate the indefinite integral.  I=sqrt(-1)

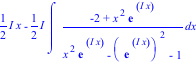
1/2*I*x-1/2*I*int((-2+x^2*exp(I*x))/(x^2*exp(I*x)-exp(I*x)^2-1), x)

> evalf(int(sin(x)/f(x),x=0...1));  Maple however can calculate the value of the definite integral over a  specified interval.

-.7529781026

>