[ Go to CENG301 Homepage | CENG301 Notes Table of Contents]
[Go to previous section: 3.1| Go
to next section: 3.3]
[ Go to CENG301 Homepage |
CENG301 Notes Table of Contents]
![]()
There are three terms that may be important in determining the
total energy in a system:
a) Potential energy
b) Kinetic energy
c) Internal energy
For a system that is a single object with mass m, these
terms are:
a) EP = mgh
b) EK = .5mv2
c) EU = m
where:
|
g = |
the gravitational field constant, |
|
h = |
the height above a datum plane of the center of the object perpendicular to the direction gravity acts, |
|
v = |
the velocity of the object relative to some "fixed" object, |
|
|
the internal energy per unit mass of the object. |
This assumes that gravity is the only field acting on the object. In
essence, the internal energy term accounts for all forms of energy
except potential and kinetic. The internal term includes the effect
of:
Note particularly that each term in this classification is measured
relative to some state or position that is considered to be the zero
point for calculating energy.
The sum of these three forms of energy is the total energy of the
object. Thus we define:
The total energy of an object may change as a result of heat
transferred to (or from) it, or by it doing work on the surroundings
(or the surroundings doing work on it). If those are the only ways
that the object's energy can change, we say that it forms a
closed system. Thus its boundaries are impervious to the flow
of mass in both directions. A system that is open has porous
boundaries so that mass can flow across them. In an open system, we
must account for the energy added to (or taken from) it by this mass
flow across its boundaries.
First, we will give the general energy balance for a closed system
expressed in terms of the change that occurs over a finite time
interval:
where:
|
ET(t) = |
the total energy of the object at time t, |
|
Q = |
the heat added to the object from time t1 to t2 and |
|
W = |
the work done by the object from time t1 to t2. |
The differential form for this is:
where:
|
q = |
the rate of heat addition to our system and |
|
w = |
the rate our system does work on the surroundings. |
The most common forms of work encountered in chemical systems
are:
a) work associated with motion acting against friction as in stirring
a liquid and
b) work associated with expansion of fluids.
The work done by an object in expanding from volume V1 to
V2 against an external pressure p is:
The energy carried into a system across its boundaries may be
categorized in the same three forms as the energy of the system
itself. If the rate of flow into the system is F mass/time then the
rate of addition of energy is:
In this expression the velocity, height and internal energy per
mass all must be evaluated at the conditions where the mass flows
across the boundary. This motion also has a work term associated with
it. The rate at which work must be done by the surroundings to get
the mass into the system is:
where:
|
|
the specific volume of the fluid |
|
p = |
the pressure |
Thus the sum of the rate of addition of energy carried in and the
work done in getting it in is:
The last two terms in this expression are usually combined as:
If we have a product stream that flows out of the system at a rate
Fout, it carries energy with it and the system must be
doing work to get it out. That looks the same as for a feed:
where we have put the superscript out on terms to indicate
that they must be evaluated at exit conditions.
All of the open systems that we encounter in this course are
steady state systems in which the total energy of the system is
constant. Then for such a system (since dET/dt = 0) our
energy balance looks like:
where w' is the rate of work the system is doing excluding the
work associated with the flows in and out of the system.
Flows in the feed and product streams at steady state system must be
equal since mass is conserved:
so we could combine the terms inside the two sets of brackets. In
a more general system with several inlet and exit streams there is no
particular advantage to be taken of this property. For our general
steady state system our balance equation expressed in mass units
is:
where:
|
j |
designates the jth stream in or out of the system and |
|
Fj |
is positive for feed streams and negative for product streams. |
If we wish to calculate the energy in our streams in terms of molar
rates, our balance will look like:
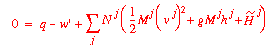
where:
|
Nj = |
the molar flow rate in stream j (positive for a feed and negative for a product stream) |
|
|
the molar specific enthalpy of a fluid. |
|
Mj = |
the average molecular weight of stream j. |
In most chemical systems like reactors and separators the kinetic
and potential energy components in the balance are unimportant so
that the balance reduces to:
If we insist on flow rates that are positive, we can split our sum
in this equation into two parts:
The calculation of the molar specific enthalpy of a fluid is
considered in the section of these notes on energy balances.